Digital Circuit

Digital Circuit

Credit to《Digital Design and Computer Architecture, Second Edition》🤯 Let’s quickly review this subject. The diagram is powered by @drawio

催更｜辅导｜私塾兼职｜联系偷偷：LifeGoesOn_Rio

1. Logic Gates

第一章主要认识最基础的逻辑门元件，然后熟悉其对应的真值表(Truth Table),主要是为第二章的组合电路(combinational circuit)做铺垫。

NOT 门（非门）: 输出是输入的逻辑反， $Y = \neg A$

BUF 门（缓冲器）: 输出与输入相同，用于信号强化。$Y = A$

AND 门（与门）: 所有输入均为1时，输出才为1。$Y = A \cap B$

OR 门（或门）: 任意输入为1时，输出为1。$Y = A \cup B$

逻辑门1

NAND 门（与非门）: 与门输出取反。 $ Y = \neg (A \cap B) $

NOR 门（或非门）: 或门输出取反。 $ Y = \neg (A \cup B) $

XOR 门（异或门）: 相异为1，相同为0。 $ Y = A \oplus B $

XNOR 门（同或门）: 相同为0，相异为1。 $ Y = \neg (A \oplus B) $

逻辑门2

三态缓冲器（tristate buffer） 是一种数字电路元件，其输出可以处于三种状态之一：高电平（1）、低电平（0）或高阻态（Z）。高阻态表示输出像断开一样，不驱动任何电流，可以用于总线控制等应用。

高水平有效（Active High）

在高水平有效的三态缓冲器中，当控制信号为高电平（1）时，缓冲器输出有效，即输出输入信号的值。当控制信号为低电平（0）时，缓冲器输出高阻态（Z）。

  • 控制信号 = 1：输出 = 输入信号
  • 控制信号 = 0：输出 = 高阻态（Z）

低水平有效（Active Low）

在低水平有效的三态缓冲器中，当控制信号为低电平（0）时，缓冲器输出有效，即输出输入信号的值。当控制信号为高电平（1）时，缓冲器输出高阻态（Z）。

  • 控制信号 = 0：输出 = 输入信号
  • 控制信号 = 1：输出 = 高阻态（Z）

逻辑门3

2. Combinational Circuit

组合电路（Combinational Circuit）是一种数字电路，其中输出仅依赖于当前输入，而不依赖于之前的输入状态。这意味着组合电路没有存储元件，因此它没有记忆功能。其主要特性包括：

  • 无记忆功能：输出仅由当前输入决定，与之前的输入无关。

  • 固定的逻辑功能：根据输入信号的组合，输出信号以确定的方式变化。

  • 构建简单：组合电路通常由基本逻辑门（如AND、OR、NOT、NAND、NOR、XOR、XNOR）构建，可以用来实现任意逻辑功能。

在有逻辑门的基础知识下，还需要有布尔表达式以及卡诺图的基础下才能完成组合电路的设计。

2.1 Boolean Equation

与或式（Sum of Products, SOP） 是一种布尔表达式形式，表示多个与项（积项）之间的或操作。每个积项由一个或多个变量通过与操作连接而成。与或式通常用于表达布尔函数的标准形式之一。例如：

$ Y = A \cdot B + \overline{A} \cdot C + B \cdot \overline{C} $

或与式（Product of Sums, POS） 是布尔表达式的另一种形式，表示多个或项（和项）之间的与操作。每个和项由一个或多个变量通过或操作连接而成。或与式也常用于表达布尔函数的标准形式之一。例如：

$ Y = (A + B) \cdot (\overline {A} + C) \cdot (B + \overline{C}) $

最小项 (Minterms) 是布尔函数的标准形式之一，其中每个最小项对应一个输出为1的输入组合。最小项由所有变量的与运算构成，每个变量可能是原变量或其补变量。通俗解释就是输出为1对应积项为1的累加。

示例：考虑一个布尔函数 ( F(A, B, C) )：

  • 当 ( A = 1 ), ( B = 0 ), ( C = 1 ) 时，最小项为 $ ( A \cdot \overline{B} \cdot C )$
  • 当 ( A = 0 ), ( B = 1 ), ( C = 0 ) 时，最小项为 $ ( \overline{A} \cdot B \cdot \overline{C} )$

假设布尔函数在以下输入组合下输出为1：

A B C F
0 0 1 1
0 1 0 1
1 0 1 1

相应的最小项表示为：

$ F(A, B, C) = \overline{A} \cdot \overline{B} \cdot C + \overline{A} \cdot B \cdot \overline{C} + A \cdot \overline{B} \cdot C $

最大项 (Maxterms) 是布尔函数的另一种标准形式，其中每个最大项对应一个输出为0的输入组合。最大项由所有变量的或运算构成，每个变量可能是原变量或其补变量。通俗解释就是输入为0所对应的和项为0的累乘

示例：同样考虑布尔函数 ( F(A, B, C) )：

这两个组合对应的最大项为：

  • 当 ( A = 0 ), ( B = 0 ), ( C = 0 ) 时，最大项为$ (A + B + C) $
  • 当 ( A = 1 ), ( B = 0 ), ( C = 1 ) 时，最大项为$ (\overline{A} + B + \overline{C} ) $

假设布尔函数 ( F(A, B, C) ) 在以下输入组合下输出为0：

A B C F
0 0 0 0
1 1 0 0

因此，相应的最大项表达式为：

\[ F(A, B, C) = (A + B + C) \cdot (\overline{A} + \overline{B} + C) \]

总结

  • 最小项：布尔函数输出为1时，对应输入组合的与运算。
  • 最大项：布尔函数输出为0时，对应输入组合的或运算。

这些概念在布尔代数和数字电路设计中非常有用，也是这门课的高频考点

2.2 Boolean Operation Rules

布尔运算的基本定律，和卡诺图一样，是逻辑电路化简的主要手段

2.2.1 交换律（Commutative Law）

交换律表示在布尔运算中，操作数的位置可以互换。

  • 与运算：$ A \cdot B = B \cdot A $
  • 或运算：$ A + B = B + A $

2.2.2 结合律（Associative Law）

结合律表示在布尔运算中，操作数的组合方式不影响运算结果。

  • 与运算：$ (A \cdot B) \cdot C = A \cdot (B \cdot C) $
  • 或运算：$ (A + B) + C = A + (B + C) $

2.2.3 分配律（Distributive Law）

分配律表示一种运算可以分配到另一种运算上。

  • 与对或：$ A \cdot (B + C) = (A \cdot B) + (A \cdot C) $
  • 或对与：$ A + (B \cdot C) = (A + B) \cdot (A + C) $

2.2.4 吸收律（Absorption Law）

吸收律表示通过某些布尔运算可以简化表达式。

  • $ A + (A \cdot B) = A $
  • $ A \cdot (A + B) = A $

2.2.5 合并律（Combining Law）

合并律表示布尔变量和其补变量的某些组合具有特定的结果。

  • $ A + \overline{A} = 1 $
  • $ A \cdot \overline{A} = 0 $

2.2.6 一致律（Identity Law）

一致律表示布尔变量与1和0的运算结果。

  • 与1：$ A \cdot 1 = A $
  • 与0：$ A \cdot 0 = 0 $
  • 或1：$ A + 1 = 1 $
  • 或0：$ A + 0 = A $

2.2.7 德摩根律（De Morgan’s Laws）

德摩根律表示对布尔表达式取反的规则。

  • $ \overline{A \cdot B} = \overline{A} + \overline{B} $
  • $ \overline{A + B} = \overline{A} \cdot \overline{B} $

2.2.8 部分二级公式推导

  • $ A + \overline{A}B = A + B$

证明: $A(1 + B) + {A}B = A + AB + \overline{A}B = A + B $

  • $ (A + B) \cdot (A + C) = A + (B \cdot C) $

证明: $ AA + AC + AB + BC = A + AB + AC + BC = A(1 + B + C) + BC = A + BC $

  • $A \cdot (A + B) = A$

证明: $AA + AB = A + AB = A(1 + B) = A$

  • $BC + B\overline{C} = B$

证明: $B \cdot (C + \overline{C}) = B \cdot 1 = B$

  • $(A + B) \cdot (A + \overline{B}) = A$

证明: $AA + A\overline{B} + AB + B\overline{B} = A + A(B + \overline{B}) = A + A = A$

  • $AB + \overline{A}C + BC = AB + \overline{A}C$

证明关键：使用吸收律 $A + AB = A$, 推广为$AB + ABC = AB$

$$
\begin{aligned}
&AB + \overline{A}C + BC \\
&= AB + \overline{A}C + (A + \overline{A})BC \\
&= AB + \overline{A}C + ABC + \overline{A}CB \\
&= AB + ABC + \overline{A}C + \overline{A}CB \text{(使用推广公式)} \\
&= AB + \overline{A}C
\end{aligned}
$$

根据吸收律可继续推广下去：
$$AB + \overline{A}C + BC\cdot(\text{其他任何项}) = AB + \overline{A}C $$

在表达式中，无论包含 $B$ 和 $C$ 的项如何复杂（例如 $BCDEFGH$），它都不会改变整个表达式的最终结果。

渲染上述公式太折磨了！修考一般不考如此复杂的化简，一般掌握K-Map化简足够应付

2.3 K-Map

在绘制卡诺图的时候需要用到格雷码的表格。首先引入一个格雷码的概念。

2.3.1 Gray Code

格雷码（Gray Code）是一种特殊的二进制编码方式，其特点是相邻的两个数码之间仅有一位二进制数不同。格雷码的发明即是用来将误差之可能性缩减至最小，编码的方式定义为每个邻近数字都只相差一个位元，因此也称为最小差异码，可以使装置做数字步进时只更动最少的位元数以提高稳定性。

格雷码的特性

  • 相邻差一位：每个相邻编码仅一位不同，减少了转换时的误差风险。
  • 非权重编码：格雷码不按照传统二进制编码的权值（如 $1, 2, 4, 8, \dots$）累加。

2 位格雷码卡诺图

0 1
0 00 01
1 11 10

3 位格雷码卡诺图

00 01 11 10
0 000 001 011 010
1 110 111 101 100

4 位格雷码卡诺图

00 01 11 10
00 0000 0001 0011 0010
01 0110 0111 0101 0100
11 1110 1111 1101 1100
10 1010 1011 1001 1000

上述表格，无论是以x轴对称，或者y轴对称，或者中心对称，均只有1位的差异

2.3.2 卡诺图化简步骤

  1. 构建 K 图：根据布尔函数的输入变量数量，构建相应大小的 K 图：

    • 2 位变量：4 格（2×2）
    • 3 位变量：8 格（2×4）
    • 4 位变量：16 格（4×4）

横轴和纵轴的变量顺序需按照格雷码排列，以确保相邻格子之间只有一个变量不同。

  1. 填写真值表和无关项：

    • 根据逻辑函数或真值表，在 K 图中标记输出为 1 的位置。
    • 将无关项标(Don’t Care Conditions)记为 X。无关项是那些对最终结果没有影响的输入组合，可以被自由选择为 1 或 0，以帮助扩大合并区域。

  2. 寻找最大合并区域：

    • 在 K 图中，寻找可以合并的 1 和 X 区域。合并的目标是形成2 的幂次方大小的区域（例如 1、2、4、8 等格），并使每个 1 尽量包含在最大的区域中。
    • 合并时遵循以下规则：
      • 只允许合并相邻的 1 和 X（上下、左右、包围环绕相邻）。
      • 尽量优先选择包含更多无关项 X 的区域，以增加合并区域的大小。
      • 合并区域可以是矩形、正方形，甚至是环绕 K 图的封闭区域。

  3. 合并相邻项：

    • 每个合并区域中的变量中，如果某个变量在区域内既有 0 又有 1，则忽略该变量（因为它在该区域中无关紧要）。
    • 将每个合并区域的共同变量提取为一个积项。对于每个变量：
      • 如果变量在区域内始终为 1，则使用原变量（如 $A$）。
      • 如果变量在区域内始终为 0，则使用其反码（如 $\overline{A}$）。

  4. 写出最简化表达式：

    • 将所有合并区域的积项求和，得到逻辑函数的最简化形式。
    • 所有包含在化简表达式中的项应尽量少，以确保表达式是最简形式。

多练多化简就行了，没什么难度

2.4 常见数字模块

这一小节跟计算机组成中的算术运算关联度很高，数字电路就是来讲解计算机所呈现出来的算术运算在底层是如何用逻辑元器件实现的。

2.4.1 Half Adder

半加器 (Half Adder) 是一个基本的数字电路，用于计算两个单比特二进制数的和。它的功能是执行二进制加法，并且产生两个输出：

  • Sum：表示两个输入二进制数加法的结果（不考虑进位）。这里用$S$来表示和。
  • Carry：表示加法结果中产生的进位。这里用$Cout$来表示产生的进位了。

根据如下K-Map我们可以得出和与进位的表达式，分别为：$S = A \oplus B$ , $Cout = A\cdot B$，再把组合电路进行封装📦(encapsulation)可以得到半加器这个电路元件
半加器

2.4.2 Full Adder

全加器 (Full Adder) 是数字电路中的一种基本元件，用于对二进制数进行加法运算。与半加器（Half Adder）相比，全加器可以对两个二进制数和一个进位位进行加法运算，并输出结果和新的进位位。

全加器的输入包括三个位：

  • A（第一个加数位）

  • B（第二个加数位）

  • Cin（输入进位位）

全加器的输出包括两个位：

  • S（和位）：表示加法结果的当前位。

  • Cout（输出进位位）：表示加法结果的进位位。

全加器

首先分析真值表写出最小项表达式，对于$S$有：

$$
\begin{aligned}
S &= \overline{A} \cdot B \cdot \overline{C_{in}} + A \cdot\overline{B} \cdot \overline{C_{in}} + \overline{A} \cdot \overline{B} \cdot C_{in} + A \cdot B \cdot C_{in} \\
&= \overline{C_{in}}(A \oplus B) + C_{in} \overline{(A \oplus B)} \\
&= A \oplus B \oplus C_{in}
\end{aligned}
$$

对于$C_{out}$有：

$$
\begin{aligned}
C_{out} &= AB \overline{C_{in}} + \overline{A}BC_{in} + A \overline{B}C_{in} + ABC_{in} \\
&= AB + C_{in}(A \oplus B)
\end{aligned}
$$

思考🤔 ：为什么黑书给的是 $C_{out} = AB + AC_{in} + BC_{in}$ ，这时候可以借助K-Map化简：如下图所示

k-map

根据K-Map化简，我们的全加器的画法会得出上图的电路，而如果根据真值表进行表达式化简，我们会得到下图的全加器。

Full Adder

我们可以用2个半加器和一个或门封装成一个全加器,具体的计算过程就不赘述了，这是修考重点！

全加器封装

2.4.3 Ripple-Carry Adder

Ripple-Carry Adder （行波进位加法器）是一种用于二进制数加法的简单组合逻辑电路，由多个一位全加器（Full Adder）级联而成，每个全加器负责处理输入位和进位。

  1. 组成结构

    • Ripple-Carry Adder 包括 $n$ 个全加器，用于计算 $n$ 位二进制数的加法。
    • 每个全加器接收两个输入位 $A[i]$ 和 $B[i]$，以及前一位的进位 $C[i]$。
    • 输出为和 $S[i]$ 和进位 $C[i+1]$。

  2. 进位传播

    • 第一个全加器处理最低有效位 $A[0]$ 和 $B[0]$ 以及初始进位（通常为 0），产生和 $S[0]$ 和进位 $C[1]$。
    • 进位 $C[1]$ 传递到下一个全加器，依次类推，直到最高有效位。

  3. 优缺点

    • 优点

      • 设计简单，硬件实现容易。

    • 缺点

      • 进位传播延迟：每个全加器必须等待前一级的进位信号，导致延迟随位数线性增长，影响运算速度。

    Ripple-Carry Adder 适用于简单、低速应用；但无法满足更高速的加法需求。

4bit行波进位加法器

2.4.4 Carry-Lookahead Adder (CLA)

Carry-Lookahead Adder (CLA) ，即先行进位加法器，是一种改进的加法器*，用于快速执行二进制加法，解决 Ripple-Carry Adder 中进位传播延迟的问题。

Carry-Lookahead Adder 通过并行计算进位信号，而不依赖逐级传播，从而显著提高速度。其核心思想是利用生成信号和传播信号：

  1. 生成信号 (Generate) ：表示某一位的加法会直接产生一个进位：
    $G_i = A_i \cdot B_i$

  2. 传播信号 (Propagate) ：表示某一位的加法会将来自上一位的进位传递下去：
    $P_i = A_i + B_i$

  3. 进位计算公式 ：根据生成和传播信号，计算每一位的进位：
    $C_{i+1} = G_i + P_i \cdot C_i$ 其中，$C_0$ 是初始进位。

推导证明：
根据前面全加器的结论，我们有：

  1. 初始公式
    $$C_{i + 1} = A_{i} \cdot B_{i} + (A_{i} + B_{i}) \cdot C_{i}$$

  2. 引入生成信号和传播信号(都是已知信号)
    $$G_{i} = A_{i} \cdot B_{i}$$
    $$P_{i} = A_{i} + B_{i}$$

  3. 公式代换
    $$C_{i + 1} = G_{i} + P_{i} \cdot C_{i} \quad \text{(用 $P_{i}$ 代换 $(A_{i} + B_{i})$)}$$

那么我就可以用已知的输入$A_{0}$ ~ $A_{n-1}$和$B_{0}$ ~ $B_{n-1}$以及$C_{0}$来确定进位是什么了。比如：
$$C_{1} = G_{0} + P_{0} \cdot C_{0}$$
$$C_{2} = G_{1} + P_{1} \cdot C_{1} = G_{1} + P_{1} G_{0} + P_{1}P_{0}C_{0}$$
不断迭代我们可以得出$C_{3}$ 和$C_{4}$，甚至到$C_{n-1}$，但是！

考虑到电路的复杂程度和电路成本的情况下，我们可以稍微妥协一下，采用分块的策略，比如实现一个32bit的加法器，我们可以将四个全加器分成一个块使用上面推导出来的门电路封装成一个块打包好。然后我们就可以迅速确定当前块的进位，减少等待进位的时间。在不考虑其他门延迟的情况下

  • 不分块的情况下：需要等32次进位的传递
  • 4个为一块的情况下：只需要等$32/4 = 8$次进位传递
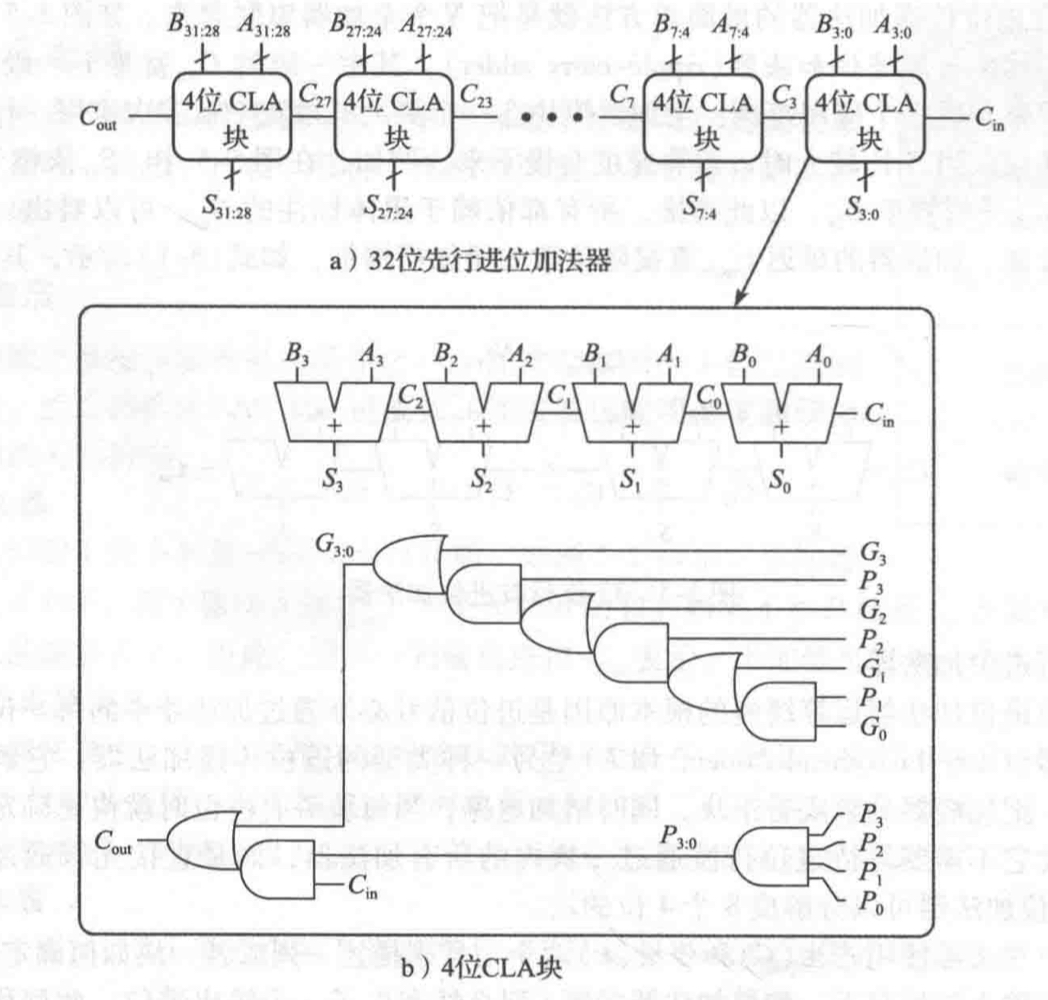
黑书: 32bit超前进位加法器

优点

  • 减少延迟：进位计算是并行完成的，速度显著快于 Ripple-Carry Adder。
  • 高效的硬件实现：适合多位二进制数加法的高速场景。

缺点

  • 硬件复杂度增加：需要额外的逻辑电路来计算生成和传播信号，随着位数增加，复杂性迅速提高。
  • 功耗较高：更多逻辑门导致功耗增加。

Carry-Lookahead Adder 是一种高效的加法器设计，常用于高速处理器中。相比 Ripple-Carry Adder，它通过并行化进位计算显著提高了运算速度，但也牺牲了一定的硬件简单性。

2.4.5 Half Subtractor

半减法器（Half Subtractor）可以对两个单个位的二进制数进行减法运算。它有两个输入：被减数$A$和减数$B$，输出包括差值（Difference, $D$）和借位（Borrow, $B_{0}$）。

  • 差值 $D = A \oplus B$

  • 借位$B_{0} = \overline{A}B$

半减法器

2.4.6 Full Subtractor

全减法器（Full Subtractor）可以对两个单个位的二进制数以及一个借位输入进行减法运算。它有三个输入：被减数$X$，减数$Y$，来自低位借位输入（Borrow_in, $B_{in}$），输出包括差值（Difference, $D$）和向高位的借位输出（Borrow_out, $B_{out}$）。

差值$D = X ⊕ Y ⊕ B_{in}$

借位输出$
B_{out}= \overline{X}B_{in} + \overline{X}Y + YB_{in}
$

上述公式可以通过真值表和K-map得出，这里就省略了

半减法器

Q：如何用N-bit全加器实现全减器？

计算机中的加减运算都是通过补码进行的，根据补码运算有$A - B$ 实现的时候可以转化为$A + (-B)$, 我们又有 $\overline{B} + 1 = -B$，所以$Y = A - B = A + \overline{B} + 1$

N-bit减法器

2.4.7 Multiplexer

复用器(Multiplexer)是一种数字电路元件，它的主要功能是将多个输入信号中的一个传递到输出端。复用器可以被视为一个多路选择开关，通过控制选择信号选择特定的输入线路。

工作原理：

  • 输入信号：有 $2^n$ 个输入信号线，每条线路可传递一个信号。
  • 选择信号：通过 $n$ 条选择线决定选取哪一个输入信号。
  • 输出信号：仅有一个输出，输出选定的输入信号。

复用器的输出可表示为：
$$
Y = I_i \quad (i \text{由选择信号确定})
$$
其中 $I_i$ 是第 $i$ 个输入。下图是一个用门电路设计2:1 MUX并封装的过程

2:1 MUX

基本结构：

  • 数据输入端（Data Inputs）：多路信号的输入端口。
  • 选择端（Select Lines）：控制信号，决定选用哪个输入。
  • 输出端（Output Line）：传递选定信号的端口。

例如：
对于一个 4路复用器（4-to-1 MUX）：

  • 有 4 个输入线：$I_0, I_1, I_2, I_3$。
  • 有 2 个选择线：$S_1, S_0$。
  • 有 1 个输出线：$Y$。

输出由选择信号 $S_1$ 和 $S_0$ 确定：

$$
Y =
\begin{cases}
I_0, & \text{if } S_1S_0 = 00 \\
I_1, & \text{if } S_1S_0 = 01 \\
I_2, & \text{if } S_1S_0 = 10 \\
I_3, & \text{if } S_1S_0 = 11
\end{cases}
$$

通过增加选择信号线数，复用器可以扩展为更大的多路选择器（如 8-to-1、16-to-1）。

MUX

2.4.8 Decoder

译码器是一种组合逻辑电路，其主要功能是将输入的二进制代码转换为独热码（one-hot code），即在输出中只有一条线路为高电平，其余为低电平。

独热码工作原理:如果有 $n$ 个类别，则需要一个长度为 $n$ 的二进制向量。对应某个类别的位置为1，其余位置为0。例如，对于3个类别：A, B, C：

  • 类别 A 编码为：$[1, 0, 0]$
  • 类别 B 编码为：$[0, 1, 0]$
  • 类别 C 编码为：$[0, 0, 1]$

译码器工作原理

  • 输入信号：有 $n$ 条输入信号线，用于表示二进制编码。
  • 输出信号：有 $2^n$ 条输出信号线，每个输出对应一种输入组合。
  • 控制信号（可选）：部分译码器可能需要使能信号（Enable），用于控制译码器的工作状态。

译码器根据输入信号的值，激活唯一对应的输出线。例如：

  • 输入：$00, 01, 10, 11$
  • 输出：$Y_0, Y_1, Y_2, Y_3$ 依次被激活。

译码器基本结构

对于一个 $n$ 位输入的译码器：

  • 有 $2^n$ 个输出信号线。
  • 每个输出信号线对应一个输入组合。

例如，一个 2-to-4 译码器（2位输入，4个输出）：

  • 输入：$A_1, A_0$。
  • 输出：$Y_0, Y_1, Y_2, Y_3$。
  • 输出逻辑：
    $$
    Y_0 = \overline{A_1} \cdot \overline{A_0}, \quad
    Y_1 = \overline{A_1} \cdot A_0, \quad
    Y_2 = A_1 \cdot \overline{A_0}, \quad
    Y_3 = A_1 \cdot A_0
    $$

译码器是数字电路中重要的基础模块，用于信号的解码与路由。

译码器
专业科目笔记
#修考 #Digital Circuit
Digital Circuit
http://toutou.zeabur.app/2024/11/04/Digital-Circuit/
Author
toutou
Posted on
November 4, 2024
Licensed under