2021年8月东大情理CS算法题解读

Author: 偷偷

尊重原创，偷偷wx:LifeGoesOn_Rio

这道题的场景是实现一个排序算法，目的是优化时间复杂度。题目的策略是使用分治递归(Divide & Conquer),在深度理解题目的场景下可以解决这道题目。

Firstly, read the pseudocode.

// return the least value that is >= kl/m
int multfrac(int k, int l, int m){
    return (k * l + (m - 1)) / m;
}

// *q <= *p
void compare_swap(int *p, int *q){
    if(*p > *q){
        int tmp = *p;
        *p = *q;
        *q = tmp;
    }
}

// sort in ascending order
void mysort(int a[], int i, int j){
    int k = j - i;  // number of elements
    if(k < 4){
        /** fill in the  blanks **/ 

    }
    else{
        mysort(a, i, i + multfrac(k, x, w));
        mysort(a, j - multfrac(k, y, w), j);
        mysort(a, i, i + multfrac(k, z, w));
    }
}

(1) 当k < 4, 即元素个数小于4时做升序排序，分类讨论即可。

if(k < 4){
    if(k <= 1) return;   // 元素个数不多于1时，不做任何处理
    else if(k == 2) compare_swap(a[i], a[i + 1]); // 比较交换一次
    else if(k == 3){
        compare_swap(a[i], a[i + 1]);
        compare_swap(a[i + 1], a[i + 2]);
        compare_swap(a[i], a[i + 1]);
    }  // 依次比较三次
}

算法详细过程如下：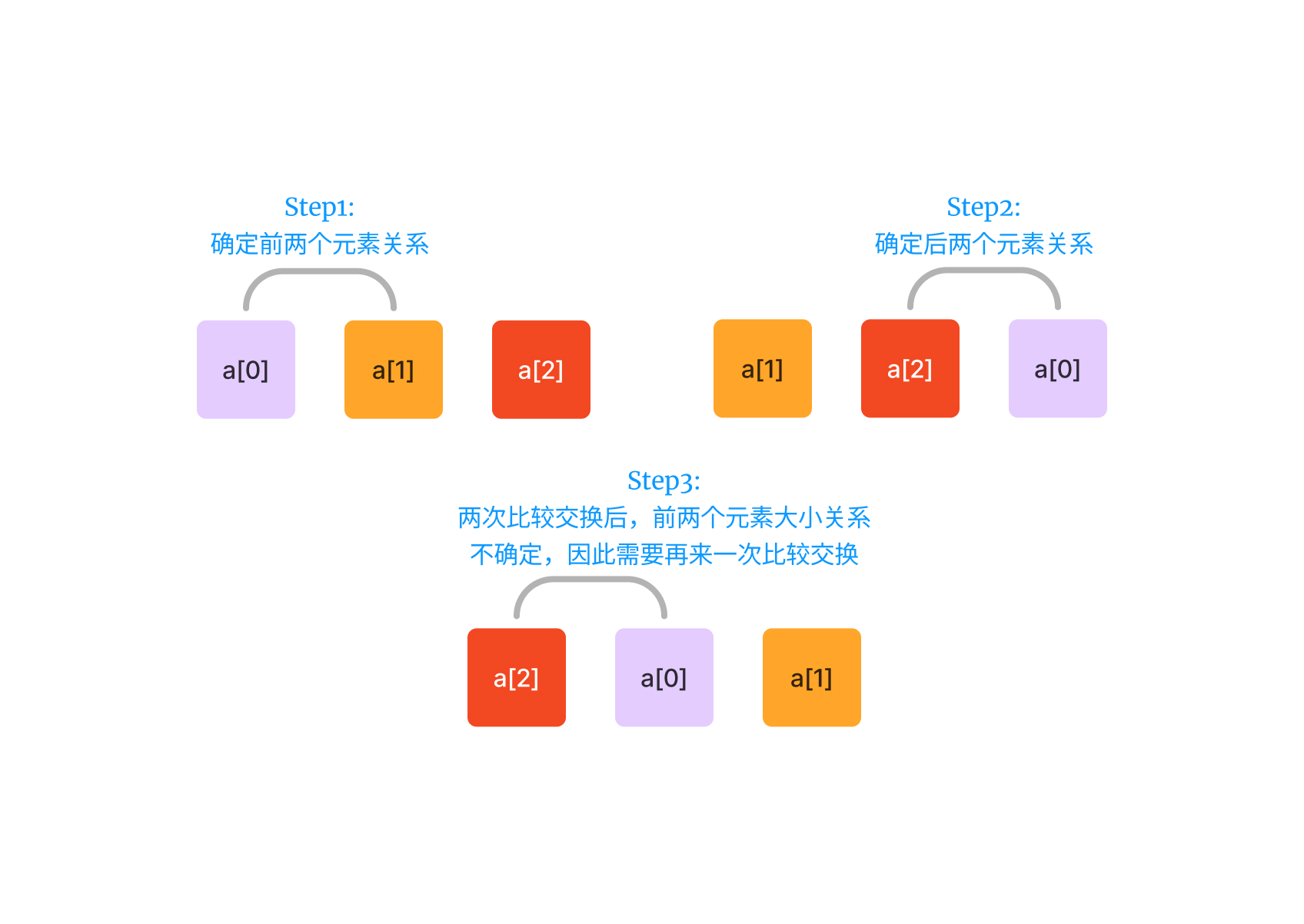

(2)

$$
T(n)=
\begin{cases}
1,\quad n\leq 3 \\
n^{\log_{4/3}{3}}, \quad n>3
\end{cases}
$$

这里也是分类讨论：

当n <= 3时，比较次数不随输入规模变化，因此为1；

当n > 3时，代入分析：

mysort(a, i, i + multfrac(k, x, w)); // sort前3/4规模的数组
mysort(a, j - multfrac(k, y, w), j); // sort后3/4规模的数组
mysort(a, i, i + multfrac(k, z, w)); // sort前3/4规模的数组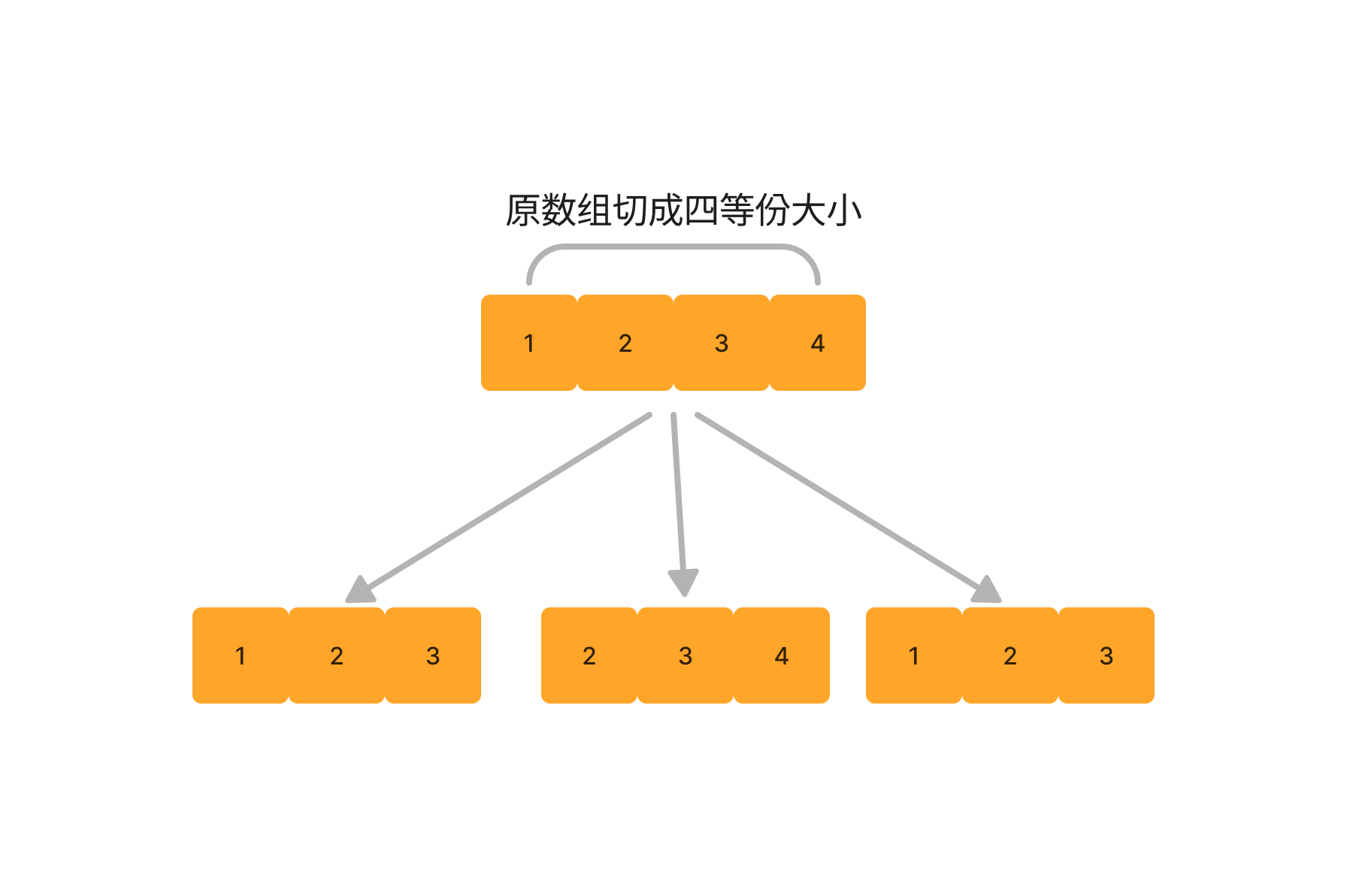

根据递归树可以写出主定理公式(Master theorem):
$$T(n) = 3T(3n/4) + O(n) $$
根据套路：这里b = 4/3, a = 3.
$$O(n ^{\log_{b}{a}}) = O(n^{log_{4/3}{3}}) > O(n) $$
所以有
$$T(n) = O(n^{\log_{4/3}{3}})$$

(3) (4, 2, 3, 3), (4, 3, 2, 3), (4, 3, 3, 2) can always work properly. (4, 2, 3, 2) can’t always work properly.

可以看下图演示：前两次的sort调用的交集部分是排好数组最大的部分，第三次sort调用要覆盖剩余没有排好的部分；对于(4, 2, 3, 2), 前两次调用排好了数组最大的1/4部分，所以第三次调用至少要覆盖数组前3/4的大小，而第三次调用只覆盖了前1/2，所以这个组合不行。

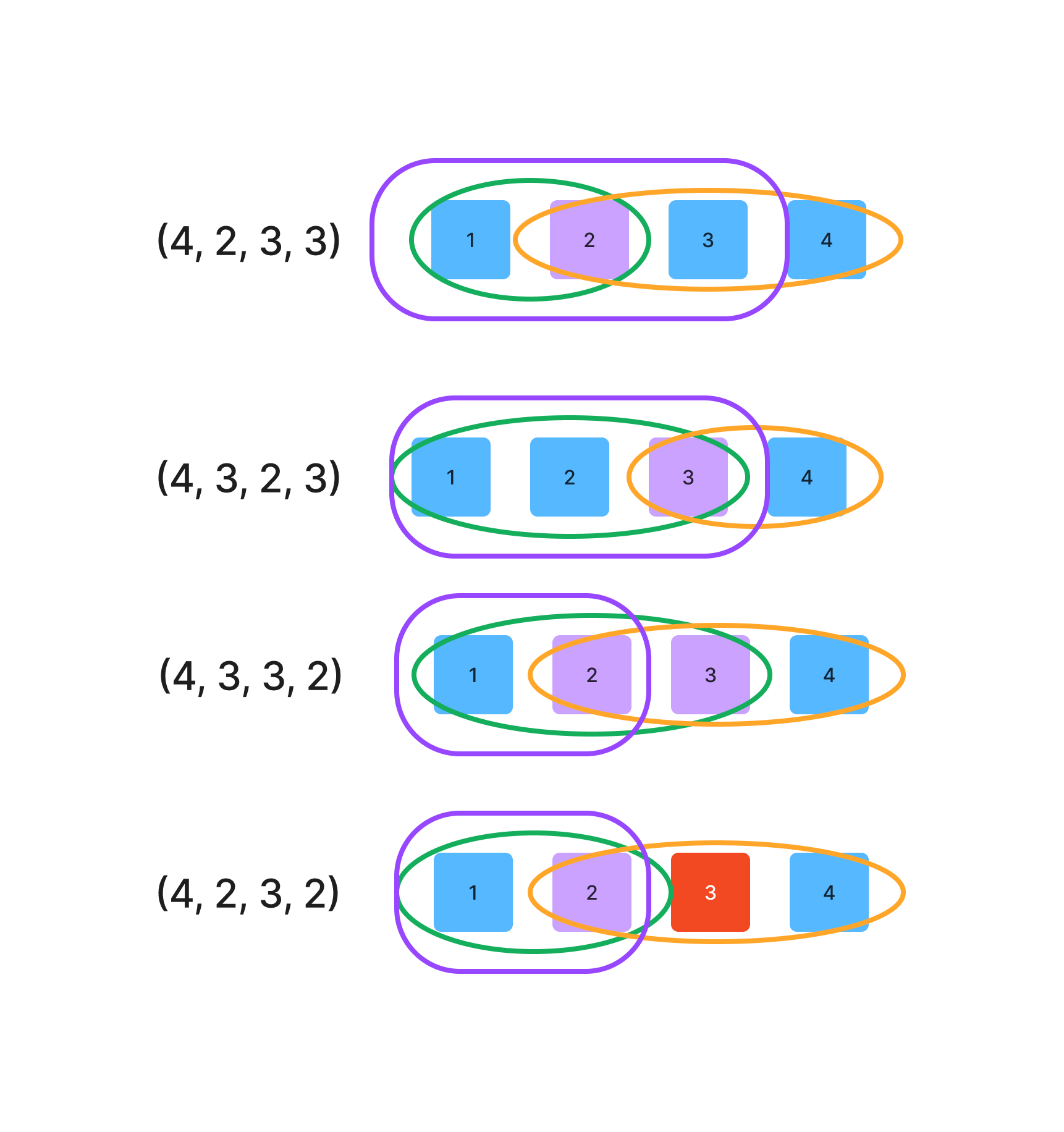
(4)
$$
\begin{cases}
x + y > w \\
x + y + z >= 2w
\end{cases}
$$

在解决第三题后，第四题就非常容易了。

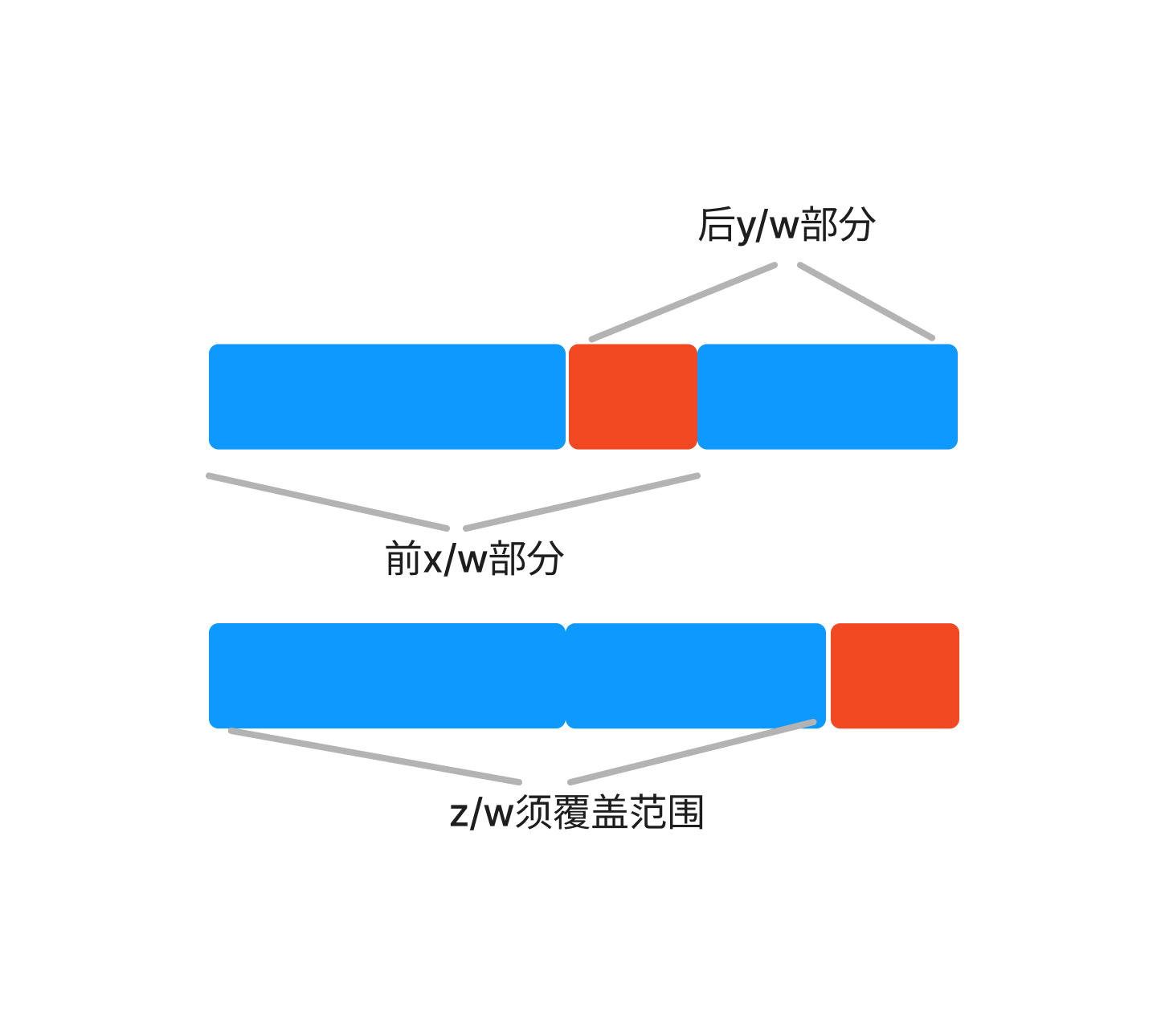
视数组的大小为1，第一次调用排好前x/w部分的元素，第二次大小排好后y/w部分的元素。所以排序需满足：

1. 前两次调用的范围必须要有交集
2. 第三次调用必须要覆盖完前两次调用的没有排好的部分。因此有：
   $$ x/ w + y / w > 1$$
   $$ z / w >= 1 - (x + y - w) / w $$